| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 자료구조 트리
- java method
- 자료구조힙
- 프로그래머스
- java
- 백준
- 개발상식
- 자바문자열
- 알고리즘
- 프렌즈4블록java
- 객체프로그래밍이란
- 공부정리
- 카카오코딩테스트
- 카카오기출
- 카카오코테
- heap
- 코딩테스트기출
- 문자열포맷
- 백준 1000번
- 백준 1000번 java
- 백준 1924번
- 자바
- 객체프로그래밍
- 프렌즈4블록
- heap정렬
- 카카오1차
- 코테준비
- Java heap
- 백준 1924번 java
- 힙정렬자바
- Today
- Total
일단 시작해보는 블로그
[알고리즘_dp] 피보나치 수열을 통한 재귀함수와 dp 본문
피보나치 수열은 dp를 이해함에 있어서 필수적인 예제이자, 이해수단(?)이다.
dp를 처음 접한다면 일단 피보나치 수열에 관련한 것을 이해한 후, 개념을 접하는 것이 혼란방지용으로 좋을 것 같다.
피보나치 수열
수학에서, 피보나치 수(fibonacci numbers)는 첫째 및 둘째 항이 1이며, 그 뒤의 모든 항은 바로 앞 두항의 합인 수열이다.
1, 1, 2, 3, 4, 7, 11, ... (1번째 항부터 나열한 피보나치 수열의 예시)
즉, 초기값 및 점화식으로 정의되어있는 규칙이 있는 수열
0행부터 정의한다면 0행의 초기값을 0으로 놓고 시작한다.

https://ko.wikipedia.org/wiki/%ED%94%BC%EB%B3%B4%EB%82%98%EC%B9%98_%EC%88%98
피보나치 수 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 피보나치 수를 이용한 사각형 채우기 수학에서, 피보나치 수(영어: Fibonacci numbers)는 첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열이다. 처음 여섯 항은 각각 1, 1, 2, 3, 5, 8이다. 편의상 0번째 항을 0으로 두기도 한다. 피보나치 수가 처음 언급된 문헌은 기원전 5세기 인도의 수학자 핑갈라가 쓴 책이다. 유럽에서 피보나치 수를 처음 연구한 것은 레오나르도 피보나치
ko.wikipedia.org
피보나치 재귀함수
재귀함수 : 자기자신을 재 호출하는 함수
피보나치 수열을 코드로 표현하면 다음과 같다.
package 재귀;
import java.util.Scanner;
public class fibonacci {
public static int fibo(int n){
if(n<=1){
return n;
}else {
return fibo(n-1) + fibo(n-2);
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
System.out.println(fibo(n));
}
}
위의 코드는 입력값인 n이 1보다 클 때, 함수 fibo 즉, 자기자신을 재호출하는 재귀함수이다.
함수의 호출은 다음과 같다. (순서는 위에서 아래로)
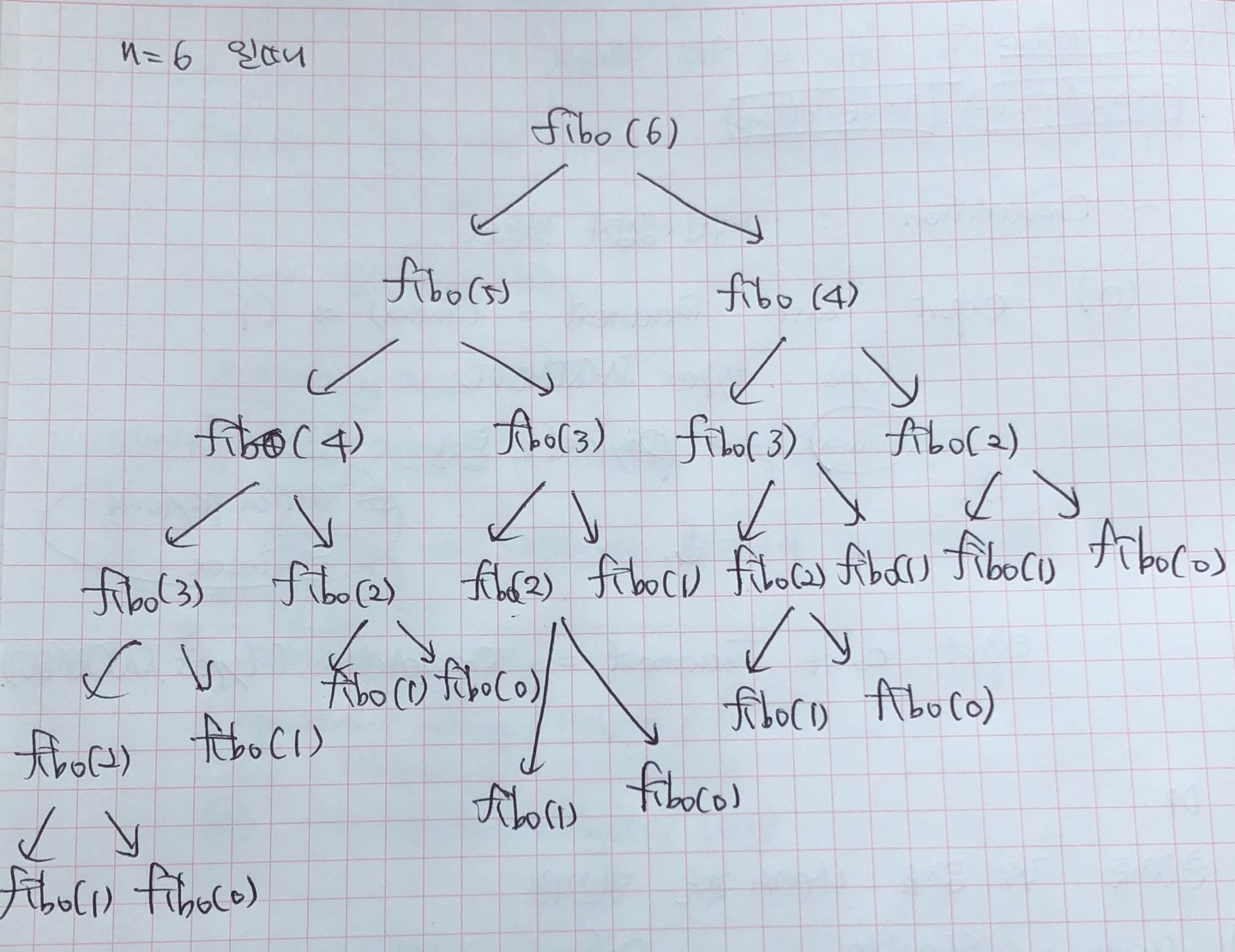
메모이제이션
메모이제이션 : 중복된 값을 재 호출할 때 최초로 선언 시, 그 값을 메모리에 저장해놨다가 꺼내쓰도록 하는 방법.
바로 위의 코드는 중복되는 함수가 많은 것을 볼 수 있다.
그렇다면 함수가 처음 호출 되었을 때 그 값을 따로 저장하여 나중에 또 다시 호출되면 그 값을 리턴하는 것이 어떨까??
실제로 이렇게 하는 기법을 메모이제이션(memoization)이라고 한다.
위의 함수는 fibo(0), fibo(1), fibo(2), fibo(3), ... ,fibo(6) 이 호출되었는데 0은 값에 아무런 영향을 주지 않으므로 패스하면 크기가 6인 배열을 만들어서 저장할 수 있게된다.
int[] d = new int[6];
이렇게 준비되었으면 다음과 같이 코딩하면 된다.
package 동적프로그래밍(dp);
import java.util.Scanner;
public class fibonacci {
static int[] d = null;
public static int fibonacci(int n){
if(d[n] > 0){
return d[n];
}
if(n<=1){
return n;
}else {
d[n] = fibonacci(n-1) + fibonacci(n-2);
return d[n];
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
d = new int[n+1];
System.out.println(fibonacci(n));
}
}

재귀함수로 구현했을 때보다 함수 호출이 확 줄어들어서 속도가 더 빨라졌을 것!
'CS > 알고리즘 개념 ' 카테고리의 다른 글
| [알고리즘_개념] 2차원 배열, 달팽이 알고리즘 (0) | 2019.09.17 |
|---|---|
| [알고리즘_개념] 2차원 배열 회전 (0) | 2019.09.17 |
| [알고리즘_개념] 2차원 배열로 다이아몬드 배열 만들기 (0) | 2019.09.17 |
| [알고리즘_개념] 재귀를 이용한 순열표현 (0) | 2019.09.10 |
| [알고리즘_개념] 비트마스크 연산, 부분집합의 표현 (2) | 2019.09.10 |




